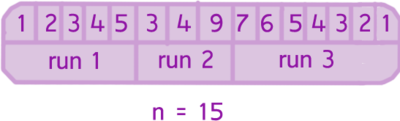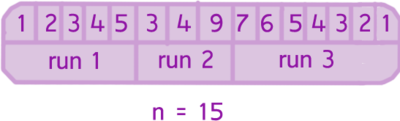
Идея: реальные данные содержат в себе уже упорядоченные подмножества, надо это использовать. Алгоритм Timsort состоит из нескольких частей:

• Шаг 1. Входной массив разделяется на подмассивы фиксированной длины, вычисляемой определённым образом.
• Шаг 2. Каждый подмассив сортируется сортировкой вставками, сортировкой пузырьком или любой другой устойчивой сортировкой.
• Шаг 3. Отсортированные подмассивы объединяются в один массив с помощью модифицированной сортировки слиянием.

Алгоритм

n — размер входного массива.

run — подмассив во входном массиве, который обязан быть упорядоченным одним из двух способов:

• строго по убыванию:

  a[i] > a[i+1] > …

• нестрого по возрастанию (неубыванию).

  a[i] ≤ a[i+1] ≤ …

<aside> 💡 Тут мы строим монотонность относительно i-го и (i+1)-го элемента. Пример: “6 -3” ⇒ далее должно быть в убывающем порядке. “6 10” ⇒ Дальше должно быть в неубывающем порядке.

</aside>

minrun — минимальный размер подмассива, описанного в предыдущем пункте.

Шаг 1. Вычисление minrun

• Шаг 1. Число minrun определяется на основе n, исходя из следующих принципов:

  1. Оно не должно быть слишком большим, поскольку к подмассиву размера minrun будет в дальнейшем применена сортировка вставками (эффективна только на небольших массивах).
  2. Оно не должно быть слишком маленьким, так как чем меньше подмассив, тем больше итераций слияния подмассивов придётся выполнить на последнем шаге алгоритма.

  Оптимальная величина для $\frac{n}{minrun}$ (количества minrun’ов) — степень двойки. Это требование обусловлено тем, что алгоритм слияния подмассивов наиболее эффективно работает на подмассивах примерно равного размера.

  Автором алгоритма было выбрано оптимальное значение, которое принадлежит диапазону [32;65)

• Шаг 2. Берем старшие 6 бит числа n и добавляем единицу, если в оставшихся младших битах есть хотя бы один ненулевой.

int minRunLength(n) {
	int flag = 0; // будет равно 1, если среди сдвинутых битов есть хотя бы один ненулевой
	while (n ⩾ 64) {
     flag = flag | (n & 1u)
     n = n >> 1u
	}
	// now 'n' has only its старшие разряды
  return n + flag
}

Шаг 2. Алгоритм разбиения на подмассивы и их сортировка

На данном этапе у нас есть входной массив, его размер n и вычисленное число minrun. Обратим внимание, что если данные изначального массива достаточно близки к случайным, то размер упорядоченных подмассивов близок к minrun. Но если в изначальных данных были упорядоченные диапазоны, то упорядоченные подмассивы могут иметь размер, превышающий minrun.

• Шаг 0. Указатель текущего элемента ставится в начало входного массива.
• Шаг 1. Начиная с текущего элемента, идет поиск во входном массиве упорядоченного подмассива run. По определению, в run однозначно войдет текущий элемент и следующий за ним. Если получившийся подмассив упорядочен по убыванию, то после вычисления run для текущего массива элементы переставляются так, чтобы они шли по возрастанию.